Question

a = 4.1 m b = 4.5 m c = 4.9 m F = 4 kN w = 3.6 kN/m Determine the support reactions at the left and rights supports. Determine the maximum bending moment and the location along the length of the beam where the maximum bending moment occurs. Given that the stress in the beam cannot exceed 96 MPa and the beam has a rectangular cross-section with a thickness of 8.7 cm, determine the minimum height of the beam.

Answer 1

Support at left = 5.99 N Support at right =15.65 N

Maximum bending moment=33.619 KNm at 9.65 m from left

Minimum height, h=0.491304 m

Step-by-step explanation:

Assuming a simply supported beam as attached

The sum of upward and downward forces are equal hence to obtain support reactions

Let reaction at the the beginning of dimension a be Ra and reaction at the end of dimension c be Rc

Ra+Rc=4+(3.6*4.9)=4+17.64=21.64

Taking sum of moments at the extreme left end support

(4.1+4.5+4.9)*Rc=4*4.1+(3.6*4.9)*(0.5*4.9+4.5+4.1)

13.5Rc=16.4+ 17.64*11.05=16.4+194.922=211.322

13.5Rc=211.322

Rc=15.65348148 rounded off as 15.65 N

Since Ra+Rc=21.64 as initially found, Ra=21.64-Rc=21.64-15.65=5.99

Maximum moment occurs when shear is zero

Equation for shear
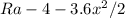`Ra-4-3.6x^(2)/2` where x is the distance from the left point where UDL starts

5.99-4=
`3.6x^(2)/2`

2*1.99=
`3.6x^(2)`

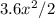
`x^(2)`=2*1.99/3.6=3.98/3.6=1.105555556

x=
`\sqrt {1.105555556}`

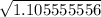
x=1.05145402

x is approximately 1.05m from the start of UDL from left.

The point of maximum shear is at 4.1+4.5+1.05m=9.65m

Maximum moment is Ra(9.65)-4(9.65-4.1)-
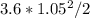`3.6*1.05^(2)/2` and substituting Ra=5.99

Maximum moment 5.99*9.65-(4*5.55)-
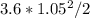`3.6*1.05^(2)/2`=33.619 KNm

Maximum moment occurs at 9.65m from extreme left and is 33.619KNm

To get maximum stress

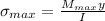`\sigma_(max)=\frac {M_(max)y}{I}` where I=
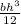`\frac {bh^(3)}{12}` and y=h/2

`\sigma_(max)=\frac {M_(max)h/2}{\frac {bh^(3)}{12} }=\frac {6M_(max)}{bh^(2)}`

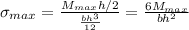
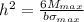`h^(2)=\frac {6M_(max)}{b\sigma_(max)}` and b is given as 8.7cm

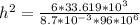
`h^(2)=\frac {6*33.619*10^(3)}{8.7*10^(-3)*96*10^(6)}`

h=
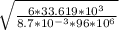`\sqrt \frac {6*33.619*10^(3)}{8.7*10^(-3)*96*10^(6)}`= 0.491304 m

h=0.491304 m