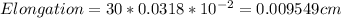Question

A rectangular aluminum bar (~1.52.1 cm in cross section) and a circular steel rod (~1 cm in radius) are each subjected to an axial force of 20 kN. Assuming that both are 30 cm long in their unloaded configuration, find (a) the stress in each, (b) the extensional strain in each, and (c) the amount of lengthening in each. Let E¼70 GPa for aluminum and 200 GPa for steel.

Answer 1

(a) Aluminium=
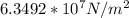`6.3492*10^(7) N/m^(2)` , steel=
`6.366*10^(7) N/m^(2)`

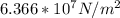
(b) Aluminium=
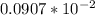`0.0907*10^(-2)` , steel=
`0.0318*10^(-2)`

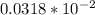
(c) Aluminium= 0.2721 cm, Steel= 0.009549cm

Step-by-step explanation:

(a)

For aluminium bar, stress,
`\sigma` is given by

`\sigma= \frac {F}{A}` where A is cross-sectional area of bar and F is force applied

Therefore,
`\sigma= \frac {20*10^(3)}{1.5*10^(-2)*2.1*10^(-2)}=6.3492*10^(7) N/m^(2)`

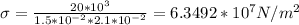
For steel rod,

`\sigma= \frac {F}{A}= \frac {20*10^(3)}{ \pi R^(2)}=\frac {20*10^(3)}{ \pi 0.01^(2)}=6.366*10^(7) N/m^(2)`

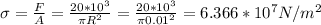
(b)

Strain,
`\epsilon` in aluminium is given by

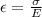`\epsilon = \frac { \sigma}{E}`where E is Young’s Modulus

`\epsilon= \frac {6.39*10^(7)}{70*10^(9)}=0.0907*10^(-2)`

For steel rod

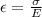
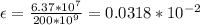
`\epsilon = \frac { \sigma}{E}`

`\epsilon= \frac {6.37*10^(7)}{200*10^(9)}=0.0318*10^(-2)`

(c)

Strain,
`\epsilon` is given by

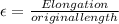`\epsilon = \frac {Elongation}{original length}` hence the change in length is product of original length and
`\epsilon`

For aluminium rod,

`Elongation= 30*0.0907*10^(-2)=0.2721 cm`

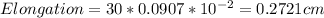
For steel rod

`Elongation= 30*0.0318*10^(-2)= 0.009549 cm`