Question

2. The Walton College of Business was ranked 24th out of all public business schools in the United States in 2005. The dean attributes this success to the academic rigor of a new core curriculum of the program. In the past, business students averaged 6.8 hours/week studying with a standard deviation of 2.2 hours. The dean wonders if students under the new curriculum are studying more than the previous students. A random sample of 100 business students finds a sample average of 7.2 hours studying. Perform the hypothesis tests for the dean at a 0.05 significance level. a. State your null and alternative hypotheses. b. Use the critical value approach to assess whether you should reject or fail to reject your null hypothesis. i. Calculate your z-statistic: ii. Identify your critical value: iii. State your conclusion: c. Compute the p-value for your z-statistic. What do you conclude when comparing your p-value to your alpha (α)? i. P-value: ii. Conclusion:

Answer 1

See steps below

Explanation:

a)

The null hypothesis is what is already established by previous researches

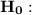`\bf H_0:` Business students average 6.8 hours/week studying.

the alternative hypothesis tries to see how accurate is this based on new evidence. Since the sample averaged 7.2 hours studying, this gives us a base to contrast the hypothesis.

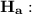`\bf H_a:` Business students now average more than 6.8 hours/week studying.

As we can see, this is a right-tailed test.

b)

For a 0.05 significance level, the critical value is the value
`\bf Z^*` such that the area under the Normal curve N(0;1) to the right of
`\bf Z^*` is less than 0.05. This is a very well-known value that can be found by looking up a table or with the computer.

`\bf Z^*`=1.64

If our z-statistic is greater or equal to 1.64 we have reasons to reject the null and accept the new average.

i.

Our z-statistic is given by the formula

`\bf z=(\bar x - \mu)/(\sigma/√(n))`

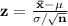
where

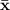`\bf \bar x` is the mean of the sample

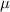`\bf \mu` is the mean of the null hypothesis

`\bf \sigma` is the standard deviation

n is the sample size

Our z-statistic is then

`\bf z=(7.2 - 6.8)/(2.2/√(100))=1.818181`

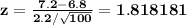
ii.

As we already said, our critical value is 1.64

iii.

Since our z-statistic is greater than the critical value, we reject the null hypothesis and accept 7.2 hours/week as the new average.

c)

The p-value for our statistic is the area under the Normal N(0;1) to the right of our z-statistic. (see picture attached).

This area can be calculated either with tables or computer-assisted and is 0.0345.

Comparing our p-value 0.0345 against the level of significance we see that

p-value < level of significance

Conclusion: when the p-value is less than the level of significance we can reject the null.

Remark:

Rejecting the null does not mean that the null is false or the alternative is true. It only means that the probability we had made a mistake by a random sampling error or other reason is less or equal than the p-value.