Question

Water flows in a 0.15-m-diameter vertical pipe at a rate of 0.20 m3/s and a pressure of 210 kPa at an elevation of 25 m. Determine (a) velocity head at elevation of 20 m, (b) pressure head at elevation of 20 m, (c) velocity head at elevation of 55 m, (d) pressure head at elevation of 55 m.

Answer 1

(a). The velocity head at elevation of 20 m is 6.52 m/s.

(b). The pressure head at elevation of 20 m is 26.42 m.

(c). The velocity is 6.52 m/s.

(d). The pressure head at elevation of 55 m is 16.42 m.

Step-by-step explanation:

Given that,

Vertical diameter = 0.15 m

Rate =0.20 m³/s

Pressure = 210 kPa

Elevation = 25 m

We need to calculate the velocity

Using formula of velocity

`Q=vA`

`v=(Q)/(A)`

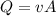
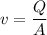
Put the value into the formula

`v=(0.20)/(\pi(D^2)/(4))`

`v=(0.20)/(\pi(0.15^2)/(4))`

`v=11.31\ m/s`

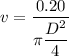
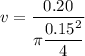
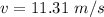
Since, Q is constant, A is constant so v will be constant everywhere.

(a). We need to calculate the velocity head at elevation of 20 m

Using formula of velocity head

`v'=(v^2)/(2g)`

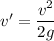
Put the value into the formula

`v'=(11.31^2)/(2*9.8)`

`v'=6.52\ m/s`

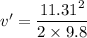
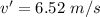
The velocity head at elevation of 20 m is 6.52 m/s.

(b). We need to calculate pressure head at elevation of 20 m,

Using Bernoulli equation

`h+(p)/(\rho g)+(v^2)/(2g)=constant`

`h+(p)/(\rho g)=constant`

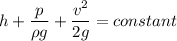
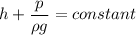
Here, velocity is constant

At h = 20 m

`20+P_(H)=25+(210*10^(3))/(1000*9.8)`

`P_{H=46.42-20`

`P_(H)=26.42\ m`

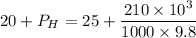
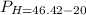
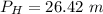
The pressure head at elevation of 20 m is 26.42 m.

(c). We need to calculate the velocity head at elevation of 55 m,

The velocity is v'=6.52 m/s.

(d). We need to calculate the pressure head at elevation of 55 m

Using formula again

At h = 55 m

`h=55+P_(H)`

`55+P_(H)=25+46.42`

`P_(H)=25-55+46.42\ m`

`P_(H)=16.42\ m`

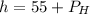
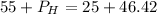
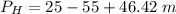
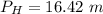
The pressure head at elevation of 55 m is 16.42 m.

Hence, this is the required solution.