Question

In a certain breed of cattle, the length of gestation has a mean of 284 days and a standard deviation is 5.5 days. One length of gestation had a z-score of -1.70. Which of the following sentences best interprets the z-score?

A. The length of this gestation period was longer than the mean length of gestation periods by 1.7 days.
B. The length of this gestation period was shorter than the mean like the gestation periods by 1.7 days.
C. The length of this gestation period was longer than the mean length of gestation periods by 1.7 standard deviations.
D. The length of this gestation period was shorter than the mean length of gestation periods by 1.7 standard deviations.

Answer 1

D. The length of the gestation period was shorter than the mean length of gestation period by 1.7 standard deviations

Explanation:

Answer 2

The statement that best interprets the z-score is;

D. The length of the gestation period was shorter than the mean length of gestation period by 1.7 standard deviations

Explanation:

The given parameters are;

The length of the gestation period of the cattle breed = 284 days

The standard deviation = 5.5 days

The z-score of one length of gestation period was z = -1.70

The formula for finding the z-score, z is presented as follows

`Z=(x-\mu )/(\sigma )`

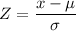
Where;

x = The observed value for the gestation period

μ = The sample mean length for the gestation period = 284

σ = The gestation period standard deviation = 5.5

When Z = -1.70, we have;

`-1.70 =(x-\mu )/(\sigma )`

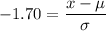
∴ x - μ = -1.7 × σ

∴ x is shorter than μ by 1.7×σ

Therefore, the length of the gestation period, x, was shorter than the mean length of gestation period, μ, by 1.7 standard deviations, σ.