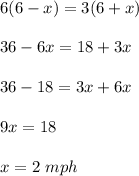Answer:
2 mph
Explanation:
The rate in still water is 6 mph. Let the rate of the water current be x mph.
Downstream:
Distance = 6 miles
Rate = 6 + x mph (current "helps")
t = unknown
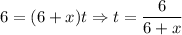
Upstream:
Distance = 3 miles
Rate = 6 - x mph (current "interferes")
t = unknown
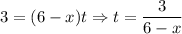
It takes the same amount of time to travel 6 miles downstream as 3 miles upstream, so
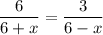
Cross multiply: