Question

Let R be the distance between the cylinder and the center of the turntable. Now assume that the cylinder is moved to a new location R/2 from the center of the turntable. Which of the following statements accurately describe the motion of the cylinder at the new location?

Answer 1

The missing statements are:

1.The speed of the cylinder has decreased.

2. The speed of the cylinder has increased.

3. The magnitude of the acceleration of the cylinder has decreased.

4. The magnitude of the acceleration of the cylinder has increased.

5. The speed and the acceleration of the cylinder have not changed.

Answer:

Only 1 and 3

Step-by-step explanation:

First of all, let's start with some definitions:

- Angular speed is the ratio between the angular displacement and the time,
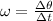`\omega = (\Delta \theta)/(\Delta t)`. Since the turntable is uniform, all the points on the disk rotates at same angular speed, so
`\omega` does not depend on the value of r

- The (tangential) speed of a point on the disk is given by

`v=\omega r`

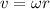
And therefore, we see that it is directly proportional to the distance from the axis, r

- Finally, the centripetal acceleration of a point on the disk is

`a=\omega^2 r`

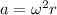
So, acceleration is proportional to r

Now we can analyze the statements. When the cylinder is moved from R to R/2 from the centre of the turntable:

1.The speed of the cylinder has decreased. --> TRUE. Because v is proportional to r, so if r decreases, v decreases as well

2. The speed of the cylinder has increased. --> FALSE. This is the opposite of 1

3. The magnitude of the acceleration of the cylinder has decreased. --> TRUE. The acceleration is also proportional to r, so since r has decreased, the acceleration also decreases

4. The magnitude of the acceleration of the cylinder has increased. --> FALSE. This is the opposite of 3

5. The speed and the acceleration of the cylinder have not changed. --> FALSE, since this is in contrast with 1 and 3.