Question

A satellite has a mass of 5832 kg and is in a circular orbit 4.13 × 105 m above the surface of a planet. The period of the orbit is 1.9 hours. The radius of the planet is 4.38 × 106 m. What would be the true weight of the satellite if it were at rest on the planet’s surface?

Answer 1

W = 28226.88 N

Step-by-step explanation:

Given,

Mass of the satellite, m = 5832 Kg

Height of the orbiting satellite from the surface, h = 4.13 x 10⁵ m

The time period of the orbit, T = 1.9 h

= 6840 s

The radius of the planet, R = 4.38 x 10⁶ m

The time period of the satellite is given by the formula

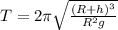`T = 2\pi \sqrt{((R+h)^(3) )/(R^(2) g) }` second

Squaring the terms and solving it for 'g'

g = 4 π²
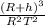`((R+h)^(3) )/(R^(2)T^(2)  )` m/s²

Substituting the values in the above equation

g = 4 π²
`((4.38X10^6+4.13X10^5)^(3) )/((4.38X10^6)^(2)X6840^(2))`

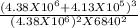
g = 4.84 m/s²

Therefore, the weight

w = m x g newton

= 5832 Kg x 4.84 m/s²

= 28226.88 N

Hence, the weight of the satellite at the surface, W = 28226.88 N