Answer:
0.0019390
Explanation:
10% of people do not like the taste of cilantro
A researcher takes a random sample of 15 people and surveys whether they like cilantro
Use the binomial distribution to compute the probability that exactly 6 of the people in the sample do not like cilantro.
Probability of success = 0.10 = p
Probability of failure = 0.9 =q
n = 15
r = 6
Formula :
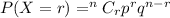
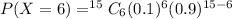
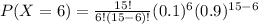
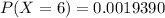
Hence the probability that exactly 6 of the people in the sample do not like cilantro is 0.0019390