Question

Healthy people have body temperatures that are normally distributed with a mean of 98.20∘F and a standard deviation of 0.62∘F . (a) If a healthy person is randomly selected, what is the probability that he or she has a temperature above 98.9∘F?

Answer 1

The probability that a healthy person has a temperature above 98.9 Fahrenheit degrees is about P(x>98.9) = 0.1292 or 12.92%.

Explanation:

This is a question of finding the probability of a normally distributed variable, and for this, we have to know that the normal distribution is determined by two parameters: the population mean and the population standard deviation. In this case, they are, respectively,
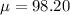`\\ \mu = 98.20` Fahrenheit degrees and
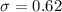`\\ \sigma = 0.62` Fahrenheit degrees.

To find probabilities, we can "transform" these "raw" scores into z-scores, or standardized values, using the z-score formula. After this, we can consult the cumulative standard normal table (available in Statistics books or on the Internet) using this z-score (e.g., z = a), for which we have the corresponding cumulative probability, that is, P(z<a). Of course, we can also use statistical software, or even a spreadsheet, to find such probabilities.

A z-score tells us the distance from the mean in standard deviations units for the standardized value of the raw score. A positive value indicates that the value is above the mean. Conversely, a negative value tells us that the value is below the mean.

The formula for this z-score is as follows

z =
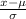`\\ (x - \mu)/(\sigma)` [1]

Where x is the raw score (x = 98.9 Fahrenheit degrees, in this case).

With this information at hand, we can solve the question.

The probability that a healthy person has a temperature above 98.9 Fahrenheit degrees

We need to find P(x>98.9).

Using formula [1], the z-score for x = 98.9 is

z =
`\\ (x - \mu)/(\sigma)`

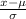
z =
`\\ (98.9 - 98.20)/(0.62)`

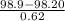
z =
`\\ (0.70)/(0.62)`

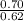
z =
`\\ 1.12903 \approx 1.13`

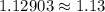
With this value for z (z = 1.13), we can consult the cumulative standard normal table to find the probability for z = 1.13 or P(z<1.13), for which we have a value of P(z<1.13) = 0.8708.

However, we are asked for P(x>98.9) = P(z>1.13), which is the complement probability for P(z<1.13) or

`\\ P(x>98.9) = P(z>1.13) = 1 - P(z<1.13)`

`\\ P(x>98.9) = P(z>1.13) = 1 - 0.8708`

`\\ P(x>98.9) = P(z>1.13) = 0.1292`

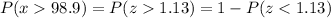
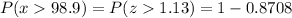
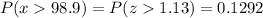
Remember that z is the standardized value for x, so P(x>98.9) = P(z>1.13).

Therefore, the probability that a healthy person has a temperature above 98.9 Fahrenheit degrees is about
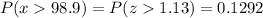`\\ P(x>98.9) = P(z>1.13) = 0.1292` or 12.92%.

We can see this area in the graph below.

Answer 2

Answer: 0.098525

Explanation:

According to the given description, we have

`\mu=98.20`

`\sigma=0.62`

Let x be a random variable that represents the body temperatures.

Also,Healthy people have body temperatures that are normally distributed.

Then , the z-score corresponds to x= 98.9 on normal curve ,

`z=(98.9-98.20)/(0.62)` (
`z=(x-\mu)/(\sigma)`)

`=1.12903225806\approx1.129`

P-value = P(x> 98.9)= P(z>1.129)=1-P(z≤1.129)

=1-0.901475=0.098525 ≈ 0.098525 (using z-value table)

Hence, the probability that he or she has a temperature above 98.9°F = 0.098525