Answer:
16172
Explanation:
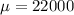
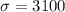
We are given that The tire manufacturer wants to offer a money-back guarantee so that no more than 3% of tires will qualify for a refund.
So, P(X≤x)=0.03
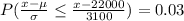
Refer the z table
So, z corresponding to p value 0.03 is -1.88
So,

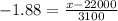
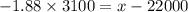
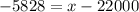


Hence the minimum number of miles the manufacturer should guarantee that the tires will last is 16172