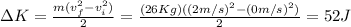Question

A box of mass 26 kg is initially at rest on a flat floor. The coefficient of kinetic friction between the box and the floor is 0.60. A woman pushes horizontally against the box with a force of 505 N until the box attains a speed of 2 m/s. What is the change in kinetic energy of the box?

Answer 1

`\Delta K = 52J`

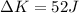
Step-by-step explanation:

The change in kinetic energy will be simply the difference between the final and initial kinetic energies:
`\Delta K=K_f-K_i`

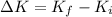
We know that the formula for the kinetic energy for an object is:

`K=(mv^2)/(2)`

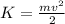
where m is the mass of the object and v its velocity.

For our case then we have:

`\Delta K = K_f-K_i=(mv_f^2)/(2)-(mv_i^2)/(2)=(m(v_f^2-v_i^2))/(2)`

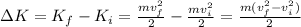
Which for our values is:

`\Delta K = (m(v_f^2-v_i^2))/(2) = ((26Kg)((2m/s)^2-(0m/s)^2))/(2) = 52J`