The distance of the corner of the base from the top of a pyramid would be = 705.72 feet
How to calculate the corner length of the given pyramid?
To calculate the corner length of the given pyramid the following steps should be taken as follows:
In a right triangle we can apply the Pythagorean Theorem to find out the length of the hypotenuse
c²=b²+a²
where
c is the hypotenuse
a and b are the legs of the right triangle (perpendicular sides)
a= 365
b= 604
c²= 365²+604²
= 133,225+364,816
= 498,041
c=
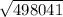
= 705.72
Therefore, the corner of the base is 705.72 feet from the top of the pyramid.