Answer:
When 6b is divided by 12 the remainder is 42 or 6b mod 12=42.
Explanation:
We suppose that b is any integer.
If 7 is the remainder left over when b is divided by 12 and we call m to the number given by the integer division
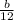
We have that
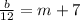
If we multiplied this expression by 6 we get a new one to calculate the remainder of
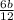
Then
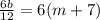 ⇒
⇒
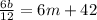
No matter what integer b we start with the remainder of
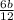 is 42.
is 42.