Question

The Michaelis constant for pancreatic lipase is 5 mM. At 60 C, lipase is subject to deactivation with a half-life of 8 min. Fat hydrolysis is carried out in a well-mixed batch reactor that simulates a top-loading washing machine. The initial fat concentration is 45 gmol m23. At the beginning of the reaction, the rate of hydrolysis is 0.07 mmol l21 s21. How long does it take for the enzyme to hydrolyse 80% of the fat present?

Answer 1

Step-by-step explanation:

According to the given data, we will calculate the following.

Half life of lipase
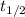`t_(1/2)` = 8 min x 60 s/min

= 480 s

Rate constant for first order reaction is as follows.

`k_(d) = (0.6932)/(480)`

=
`1.44 * 10^(-3)s^(-1)`

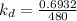
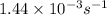
Initial fat concentration
`S_(o)` = 45
`mol/m^(3)`

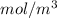
= 45 mmol/L

Rate of hydrolysis
`V_m_(o)` = 0.07 mmol/L/s

Conversion X = 0.80

Final concentration (S) =
`S_(o) (1 - X)`

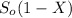
= 45 (1 - 0.80)

= 9
`mol/m^(3)`

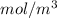
or, = 9 mmol/L

It is given that
`K_(m)` = 5mmol/L

Therefore, time taken will be calculated as follows.

t =
`-(1)/(K_(d))ln[1 - (K_(d))/(V){K_(M) ln ((S_(o))/(S)) + (S_(o) - S)]`

Now, putting the given values into the above formula as follows.

t =
`-(1)/(K_(d))ln[1 - (K_(d))/(V){K_(M) ln ((S_(o))/(S)) + (S_(o) - S)]`

=
`-(1)/(1.44 * 10^(-3)s^(-1))ln[1 - (1.44 * 10^(-3)s^(-1))/(0.07 mmol/L/s ){K_(M) ln ((45 mmol/L )/(9 mmol/L )) + (45 mmol/L - 9 mmol/L )]`

=
`1642.83 s * (1 min)/(60 sec)`

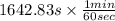
= 27.38 min

Therefore, we can conclude that time taken by the enzyme to hydrolyse 80% of the fat present is 27.38 min.