Question

Given matrices G and H below, which statement is true?

G= 7 5
4 3



H= -6 -5
-4 -2

A.) Matrices G and H are not inverses of each other because G + H does not equal I.

B.) Matrices G and H are not inverses of each other because GH does not equal I.

C.) Matrices G and H are inverses of each other because GH = I.

E.) Matrices G and H are inverses of each other because G + H = I.

Answer 1

B. Matrices G and H are not inverses of each other because GH not equal to I.

Explanation:

Answer 2

Option B.

Explanation:

The given matrices are

`G=\begin{bmatrix}7&5\\ \:4&3\end{bmatrix}`

`H=\begin{bmatrix}-6&-5\\ \:-4&-2\end{bmatrix}`

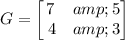
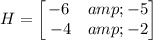
Two matrices are inverse of each other if product of both matrices is identity matrix, i.e.,
`I=\begin{bmatrix}1&0\\ \:0&1\end{bmatrix}`.

`\begin{bmatrix}7&5\\ \:4&3\end{bmatrix}\begin{bmatrix}-6&-5\\ \:-4&-2\end{bmatrix}`

`\begin{bmatrix}7\left(-6\right)+5\left(-4\right)&7\left(-5\right)+5\left(-2\right)\\ 4\left(-6\right)+3\left(-4\right)&4\left(-5\right)+3\left(-2\right)\end{bmatrix}`

`\begin{bmatrix}-62&-45\\ -36&-26\end{bmatrix}\\eq I`

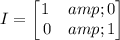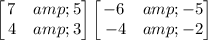
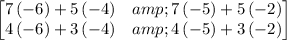
Matrices G and H are not inverses of each other because GH does not equal I.

Therefore, the correct option is B.