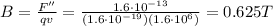Question

When at rest, a proton experiences a net electromagnetic force of magnitude 9.0×10−13 N pointing in the positive x direction. When the proton moves with a speed of 1.6×106 m/s in the positive y direction, the net electromagnetic force on it decreases in magnitude to 7.4×10−13 N , still pointing in the positive x direction Find the magnitude of the magnetic field.

Answer 1

0.625 T

Step-by-step explanation:

At first, the proton is at rest, so the force it experiences must be due to the presence of an electric field. The direction of the field is the same as the direction of the force, so along the positive x-direction. The magnitude of the force is given by:

`F=qE`

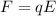
where

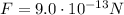`F=9.0\cdot 10^(-13) N` is the force

`q=1.6\cdot 10^(-19) C` is the charge of the proton

E is the magnitude of the electric field

Later, the proton starts moving, and the net force decreases to

`F' =7.4\cdot 10^(-13)N`

This means that there is another force acting on the proton, in the opposite direction (negative x-axis), of magnitude

`F'' = 9.0\cdot 10^(-13)-7.4\cdot 10^(-13)=1.6\cdot 10^(-13) N`

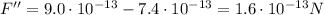
This force is due to the presence of a magnetic field, which is perpendicular to the direction of motion of the charge, so its magnitude is given by

`F''=qvB`

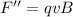
where

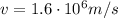`v=1.6\cdot 10^6 m/s` is the speed of the proton

B is the magnitude of the magnetic field

Solving for B, we find:

`B=(F'')/(qv)=(1.6\cdot 10^(-13))/((1.6\cdot 10^(-19))(1.6\cdot 10^6))=0.625 T`