Question

A water balloon is thrown horizontally at a speed of 2.00 m/s from the roof of a building that is 6.00 m above the ground. At the same instant the balloon is released, a second balloon is thrown straight down at 2.00 m/s from the same height. Determine which balloon hits the ground first and how much sooner it hits the ground than the other balloon. (Neglect any effects due to air resistance.)

Answer 1

• The water ballon that was thrown straight down at 2.00 m/s hits the ground first, 0.19 s before the other ballon.

Step-by-step explanation:

The motions of the two water ballons are ruled by the kinematic equations:

• 
  `y=y_0+V_0t-gt^2/2`

We are only interested in the vertical motion, so that equation is all what you need.

1. Water ballon is thrown horizontally at sped 2.00 m/s.

The time the ballon takes to hit the ground is independent of the horizontal speed.

Since 2.00 m/s is a horizontal speed, you take the initial vertical speed equal to 0.

Then:

`y=y_0+V_0t-gt^2/2\\ \\ 0=6.00m-9.8(m)/(s^2) t^2/2\\ \\ t=\sqrt{2*6.00m/9.8(m)/(s^2)}\\\\ t=1.11s`

2. Water ballon thrown straight down at 2.00 m/s

Now the initial vertical speed is 2.00 m/s down. So, the equation is:

`0=6.00m-2.00(m)/(s)t-9.8(m)/(s^2)t^2/2\\ \\ 4.9t^2+2t-6=0\\ \\ t=0.92s`

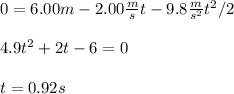
To solve the equation you can use the quadratic formula.

`t=(-2+/-√(2^2-4(4.9)(-6)) )/(2(4.9))\\ \\ t=-1.33\\ \\ t=0.92`

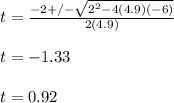
You get two times. One of the times is negative, thus it does not have physical meaning.

3. Conclusion:

The water ballon that was thrown straight down at 2.00 m/s hits the ground first by 1.11 s - 0.92s = 0.19 s.