Question

Two points, point A and point B, are situated above a current-carrying wire. Point B is located at a distance R from the wire, which is twice as far from the wire as point A. By what factor is the magnetic field at point A larger or smaller than the magnetic field at point B?

Answer 1

By a factor of 2

Step-by-step explanation:

The strength of the magnetic field produced by a current-carrying wire is given by

`B=(\mu_0 I)/(2\pi r)`

where

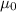`\mu_0` is the vacuum permeability

I is the current

r is the distance from the wire

At point A, which is located at a distance
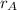`r_A` from the wire, the magnetic field strength is

`B_A = (\mu_0 I)/(2 \pi r_A)`

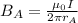
Point B is located at a distance of

`r_B = 2 r_A`

from the wire, so the strength of the field at point B is

`B_B = (\mu_0 I)/(2 \pi r_B) = (\mu_0 I)/(2 \pi (2 r_A)) = (B_A)/(2)`

Or equivalently,

`B_A =2B_B`

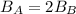
So, the field at A is twice as strong as the field at B.