Answer:
The probability of obtaining at least one 6 in four rolls of a fair die is 0.5177
The probability of obtaining at least one double six in 24 rolls of a fair die is 0.4914
Explanation:
Consider the provided information.
Part (A) What is the probability of obtaining at least one 6 in four rolls of a fair die?
The probability of getting a six in a throw of a fair die is = 1/6
The probability of not getting a six is = 5/6
Let X be the favorable outcome, that at least one 6.
To find the probability of at least one 6, subtract the probability that in 4 throws of a die no 6 is obtained from 1.
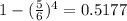
Hence, the probability of obtaining at least one 6 in four rolls of a fair die is 0.5177
Part (B) If a pair of fair dice is tossed 24 times, what is the probability of at least one double six?
Throwing two die at a time then the probability of two six is = 1/36
Throwing two die at a time then the probability of not getting two six is = 35/36
To find the probability of at least one double 6, subtract the probability that in 24 throws of a die no 6 is obtained from 1.
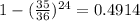
Hence, the probability of obtaining at least one double six in 24 rolls of a fair die is 0.4914