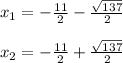Answer:
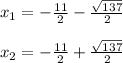
Explanation:
Given the following quadratic equation:
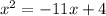
The steps to solve it are:
1. Move the terms to one side of the equation:
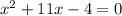
2. Apply the Quadratic formula
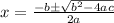 .
.
In this case we can identify that:
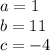
Then, substituting these values into the Quadratic formula we get the following solutions: