Question

A water tower is idealized as a mass M on top of a uniform and massless beam. The bottom end of the beam is fixed to the ground. The beam has solid circular cross section with a diameter of 1.2 m. Its Young’s modulus is 30 GPa, and its length is 10 m. The mass M is 20 tons. Find the natural frequency and natural period of this system in lateral oscillations.

Answer 1

Natural frequency=21.40 Hz

Time= 0.2936 seconds

Step-by-step explanation:

Idealizing the question as a cantilever beam with point load of mass M as 20 tons

Lateral stiffness,
`k=\frac {3EI}{l^(3)}` where l is length given as 10 m, E is Young’s modulus given as 30GPa and I is inertia where for a circular cross-section is given by
`\frac {\pi d^(4)}{64}`

k=
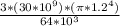`\frac {3*(30*10^(9))*(\pi *1.2^(4))}{64*10^(3)}`= 9160884.178

k=
`9.160884178*10^(6)`

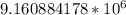
To find the frequency,
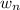`w_(n)`, the mass m is given as 20 tons or 20000 Kg

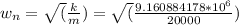`w_(n)=\sqrt (\frac {k}{m})= \sqrt (\frac {9.160884178*10^(6)}{20000})`=21.40196741 Hz

Natural frequency=21.40 Hz

Time period,

T=
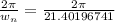`\frac {2\pi}{w_(n)}=\frac {2\pi}{21.40196741}`=0.2935798 seconds

T=0.2936 seconds