Question

Innocent until proven guilty? In Japanese criminal trials, about 95% of the defendants are found guilty. In the United States, about 60% of the defendants are found guilty in criminal trials†. Suppose you are a news reporter following ten criminal trials. (a) If the trials were in Japan, what is the probability that all the defendants would be found guilty?

Answer 1

The probability that all the defendants would be found guilty is 60% (P=0.5987).

Explanation:

We can model this as a binomial distribution problem.

In Japan 95% of the defendants are found guilty, so there is a probability of 5% of being found innocent.

We can calculate the probability of having none of them found innocent as:

`P(I=k)=(n!)/(k!(n-k)!)*p^k*(1-p)^(n-k) \\\\P(I=0)=(10!)/(0!10!)*0.05^0*0.95^(10)\\\\P(I=0)=1*1*0.5987\\\\P(I=0)=0.5987`

Answer 2

1

Explanation:

This situation can be modeled with the Binomial Distribution which gives the probability of an event that occurs exactly k times out of n, and is given by

`\large P(k;n)=\binom{n}{k}p^kq^(n-k)`

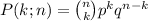
where

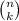`\large \binom{n}{k}`= combination of n elements taken k at a time.

p = probability that the event (“success”) occurs once

q = 1-p

In this case, the event “success” is finding a defendant guilty (in Japan) with probability 95% = 0.95 (9.5 out of 10) and n=10 criminal trials randomly chosen.

“If the trials were in Japan, what is the probability that all the defendants would be found guilty?”

Since P(0;10) is the likelihood that none of the defendants is found guilty, we want the complement 1-P(0;10)

but

`\large P(0;10)=0.05^(10)=9.7656*10^(-14)`

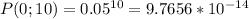
that for practical effects, can be considered equals 0, so the probability that all the defendants will be found guilty in 10 cases in Japan is practically 1.