Question

A randomly selected sample of n = 12 students at a university is asked, \How much did you spend for textbooks this semester?" The responses, in dollars, are 200, 175, 450, 300, 350, 250, 150, 200, 320, 370, 404, 250 (a). Construct an approximate 95% confidence interval for the population mean using the CLT. (b). If the data are assumed from N(µ; σ2), construct an exact 95% confidence interval for the population mean.

Answer 1

a) [92.8 , 477.04]

b) [69.611, 500.229]

Explanation:

The mean and standard deviation of the sample can be computed by using the definition formulas and we obtain

mean

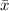`\large \bar x` = 284.9165 ≅ $284.92

standard deviation

s = 96.0639 ≅ $96.06

a)

Roughly speaking, we could say that a 95% confidence interval is given by the 68–95–99.7 rule for the Normal Distribution, which states that around 95% of the data is between
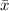`\large \bar x` -2s and
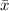`\large \bar x` +2s. So, an informal 95% confidence interval would be

[284.92 - 2*96.06, 284.92 + 2*96.06] = [92.8 , 477.04]

b) If the data are assumed from
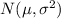`\large N(\mu ,\sigma ^2)`, then the 95% confidence interval is given by [A, B] where A, B are values such that the area under the normal curve
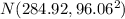`\large N(284.92 ,96.06 ^2)` outside the interval [A, B] is less than 5% or 0.05 (see picture attached).

This value can be found with the help of a calculator or computer, and we find

[A, B] = [69.611, 500.229]