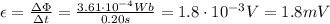Question

A long solenoid of length 9.10 × 10-2 m and cross-sectional area 5.0 × 10-5 m2 contains 6500 turns per meter of length. Determine the magnitude of the emf induced in the solenoid when the current in the solenoid changes from 0 to 1.5 A during the time interval from 0 to 0.20 s.

Answer 1

1.8 mV

Step-by-step explanation:

The total number of turns in the solenoid is

`N=nL = (6500)(9.10\cdot 10^(-2))=592`

where

n = 6500 is the number of turns per meter of length

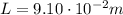`L=9.10\cdot 10^(-2) m` is the length of the solenoid

The flux linkage through the solenoid is given by

`\Phi = NBA`

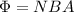
where

B is the strength of the magnetic field

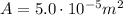`A=5.0\cdot 10^(-5)m^2` is the cross-sectional area of the solenoid

The strength of the field in the solenoid is given by

`B=\mu_0 n I`

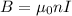
where I is the current.

At the beginning, I = 0, so the field is

`B_i=0`

And the flux linkage is

`\Phi_i = NAB_i = 0`

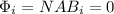
Later, the current is I = 1.5 A, so the field in the solenoid is

`B_f = (4\pi \cdot 10^(-7))(6500)(1.5)=0.0122 T`

So, the flux linkage is

`\Phi_f = (592)(5.0\cdot 10^(-5))(0.0122)=3.61\cdot 10^(-4)Wb`

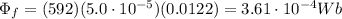
So, the change in flux linkage is

`\Delta \Phi = \Phi_f - \Phi_i = 3.61\cdot 10^(-4) Wb`

And therefore, the emf induced in the solenoid is (in magnitude)

`\epsilon=(\Delta \Phi)/(\Delta t)=(3.61\cdot 10^(-4) Wb)/(0.20 s)=1.8\cdot 10^(-3) V = 1.8 mV`