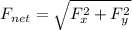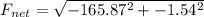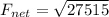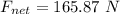Answer:
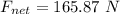
Step-by-step explanation:
given,
angle of inclination with the horizontal = 8.5°
force of gravity = 1225 N
normal force on car = 1210 N
frictional force = 15.2 N
net force = ?
equating horizontal forces

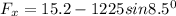
F_x = -165.87 N
equating vertical forces

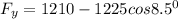
F_y = -1.54 N
net force