Question

In this video, the linear motion of the descending sphere is directly related to the rotational motion of the wheel, and in order to complete our calculations we will need to identify this connection. What is the relationship between the linear acceleration a of the descending sphere and the angular acceleration α of the rotating wheel?

Answer 1

Step-by-step explanation:

Let a is the linear acceleration of the descending sphere. It is given by,

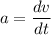`a=(dv)/(dt)`.......(1) (change in velocity)

Let
`\alpha` is the angular acceleration α of the rotating wheel. It is given by :

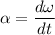`\alpha =(d\omega)/(dt)`............(2) (change in angular velocity)

Dividing equation (1) and (2) we get :

`(a)/(\alpha )=(dv)/(d\omega)`

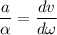
Since,
`v=r\omega`

`(a)/(\alpha )=(d(r\omega))/(d\omega)`

`(a)/(\alpha )=r`

`a=\alpha r`

`a=\alpha * r`

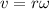
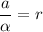
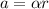
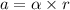
Hence, this is the required solution.