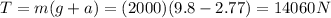Question

An elevator and its load have a combined mass of 2000 kg. Find the tension in the supporting cable when the elevator, originally moving downward at 12 m/s, is brought to rest with constant acceleration in a distance of 26 m.3

Answer 1

14060 N

Step-by-step explanation:

We start by calculating the acceleration of the elevator. This can be found using the suvat equation:

`v^2-u^2=2as`

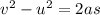
where

v = 0 is the final velocity

u = 12 m/s is the initial velocity

a is the acceleration

s = 26 m is the stopping distance

Solving for a, we find

`a=(v^2-u^2)/(2s)=(0-(12)^2)/(2(26))=-2.77 m/s^2`

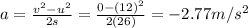
Now let's write the equation of the forces acting on the elevator. Taking upward as positive direction:

`T-mg=ma`

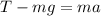
where

T is the tension in the cable

(mg) is the weight of the elevator, where

m = 2000 kg is the mass

`g=9.8 m/s^2` is the acceleration of gravity

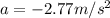`a=-2.77 m/s^2` is the deceleration

Solving for T,

`T=m(g+a)=(2000)(9.8-2.77)=14060 N`