Question

In the arithmetic sequence, -12, -17, -22, -27... which term has a value of -68?​

Answer 1

-68 is not a term in the given sequence

Explanation:

The given sequence is -12, -17, -22, -27...

There is a common difference of d=-17--12=-5

The explicit rule for this sequence is
`f(n)=-12-5(n-1)`

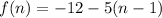
Or
`f(n)=-5n-7`

To find the term that has a value of -68 we equate the explicit formula and solve for n.

`-68=-5n-7`

`\implies -68+7=-5n`

`\implies -61=-5n`

`n=(61)/(5) =12.2`

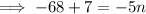
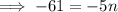
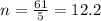
The position should be a natural number.

Since n is a decimal, it tells us that -68 is not a term in the given sequence