Question

Problem 15-7 (Algorithmic) Speedy Oil provides a single-server automobile oil change and lubrication service. Customers provide an arrival rate of 4 cars per hour. The service rate is 5 cars per hour. Assume that arrivals follow a Poisson probability distribution and that service times follow an exponential probability distribution. What is the average number of cars in the system? If required, round your answer to two decimal places

Answer 1

Answer: There are 4 average cars in the system.

Explanation:

Since we have given that

Arrival rate = λ = 4 cars per hour

Service rate = μ = 5 cars per hour

We need to find the average number of cars in the system.

So, Average number of cars would be

`L_q=(\lambda^2)/(\mu(\mu-\lambda))\\\\L_q=(4^2)/(5(5-4))\\\\L_q=(16)/(5)\\\\L_q=3.2`

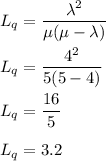
So, it becomes,

`L=L_q=(\lambda)/(\mu)\\\\L=3.2+(4)/(5)\\\\L=3.2+0.8\\\\L=4`

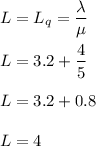
Hence, there are 4 average cars in the system.