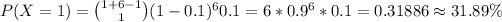Question

You are the manager of The Copy Shop. For your big copy machine, the probability a copy of a document will have a defect is 0.1. ("A defect" means one or more defects.) What is the probability that the 7th copy will be the first one with a defect? X = number of the copy that is the first one with a defect a. X ~ binomial b. X ~ negative binomial c. X ~ hypergeometric d. X ~ Poisson

Answer 1

31.89%

Explanation:

This situation can be modeled with the Negative Binomial Distribution, where the probability of having r “failures” before k “successes” occur is given by

`\large P(X=k)=\binom{k+r-1}{k}(1-p)^rp^k`

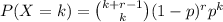
being p the probability that a “success” occurs.

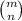`\large \binom{m}{n}` is the number of combinations of m elements taken n at a time.

In the specific case of this problem we have “success” is having a copy with a defect, with probability 0.1, k=1 and r=6 (6 “failures” before 1 “success”).

Computing the formula either by hand or with a computer, we get

`\large P(X=1)=\binom{1+6-1}{1}(1-0.1)^60.1=6*0.9^6*0.1=0.31886\approx 31.89\%`