Question

Find the probability that a roll of two dice will produce a sum of either 7 or 11

How many times would you expect this to occur in 50 trials?

Answer 1

`(2)/(9)`

11 times

Explanation:

When you roll two number dice, you can get 36 different outcomes:

`\begin{array}{cccccc}(1,1)&(1,2)&(1,3)&(1,4)&(1,5)&(1,6)\\(2,1)&(2,2)&(2,3)&(2,4)&(2,5)&(2,6)\\(3,1)&(3,2)&(3,3)&(3,4)&(3,5)&(3,6)\\(4,1)&(4,2)&(4,3)&(4,4)&(4,5)&(14,6)\\(5,1)&(5,2)&(5,3)&(5,4)&(5,5)&(5,6)\\(6,1)&(6,2)&(6,3)&(6,4)&(6,5)&(6,6)\end{array}`

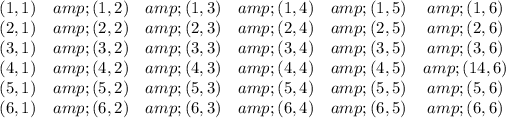
The sum of 7 give outcomes:

`(1,6),\ (2,5),\ (3,4),\ (4,3),\ (5,2),\ (6,1)`

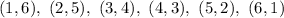
- 6 outcomes in total.

The sum of 11 give outcomes:

`(5,6),\ (6,5)`

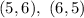
- 2 outcomes in total.

So, the probability that a roll of two dice will produce a sum of either 7 or 11 is

`(6+2)/(36)=(8)/(36)=(2)/(9)`

In 50 trials, you can expect

`(2)/(9)\cdot 50=(100)/(9)=11(1)/(9)\approx 11`

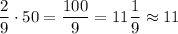
times this event to occur