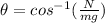Question

A car is traveling up a hill that is inclined at an angle of θ above the horizontal. (d) What is the algebraic expression for the ratio of the magnitude of the normal force to the weight of the car? Express your answer in terms of the angle θ at which the hill is inclined. Ratio =

Answer 1

`\theta= cos^(-1)(\frac {N}{mg})`

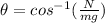
Step-by-step explanation:

From the attached sketch where the box represents a car travelling up a hill. The normal force of the car
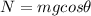`N=mgcos \theta` where m is the mass of the car and g is the gravitational constant

This can be re-written as
`cos\theta= \frac {N}{mg}`

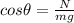
Getting the inverse of
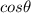`cos\theta` we have
`\theta= cos^(-1)(\frac {N}{mg})`

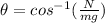
From the diagram also, the ratio of normal force to weight is
`cos\theta`

`\frac {mg cos\theta}{mg}=cos\theta`

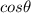
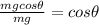
Conclusively,
`\theta= cos^(-1)(\frac {N}{mg})`