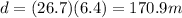Question

A plane dives at 43° to the horizontal and releases a package at an altitude of 360m. If the load is in the air for 6.4s, find: a)the speed of the plane when it released the package b) the horizontal distance traveled by the package after it is released.

Answer 1

a) 36.5 m/s

The motion of the package along the vertical direction is a free fall motion, so we can use the following suvat equation:

`s=u_y t + (1)/(2)gt^2`

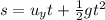
where, chosing downward as positive direction:

s = 360 m is the vertical displacement of the package

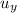`u_y` is the initial vertical velocity of the package, which is equal to that of the plane

t = 6.4 s is the time of flight

`g=9.8 m/s^2` is the acceleration of gravity

Solving for
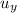`u_y`, we find:

`u_y = (s)/(t)-(1)/(2)gt=(360)/(6.4)-(1)/(2)(9.8)(6.4)=24.9 m/s`

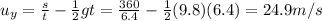
The initial vertical velocity is related to the initial speed of the plane by

`u_y = u sin \theta`

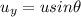
where

u is the initial speed of the plane

`\theta=43^(\circ)`

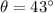
Solving for u,

`u=(u_y)/(sin \theta)=(24.9)/(sin 43)=36.5 m/s`

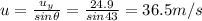
b) 170.9 m

The horizontal velocity of the package is given by

`v_x = u cos \theta = (36.5)(cos 43)=26.7 m/s`

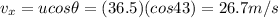
where

u = 36.5 m/s is the initial speed

`\theta=43^(\circ)`

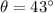
The horizontal velocity of the package is constant since there are no forces along this direction: therefore, the horizontal distance travelled by the package is given by

`d=v_x t`

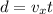
And substituting t = 6.4 s, we find

`d=(26.7)(6.4)=170.9 m`