Answer:
C.
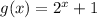
Explanation:
We know that the parent function is
 .
.
Now, the function that the graph shows intercepts
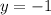 , and the problem states that is the reflection of
, and the problem states that is the reflection of
 across the x-axis. That means the original function has to intercept
across the x-axis. That means the original function has to intercept
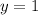 , which is the reflected interception of
, which is the reflected interception of
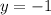 .
.
We also know that y-interceptions are shown as independent terms, so the function
 is defined as follows
is defined as follows
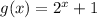
Where
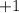 represent the y-interception.
represent the y-interception.
The graph of
 is attached. The red curve represents
is attached. The red curve represents
 and the blue curve represents
and the blue curve represents
 . You can observe that models exactly the function we are looking for.
. You can observe that models exactly the function we are looking for.