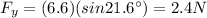Question

A dog pulls on a pillow with a force of 6.6 N at an angle of 21.6 ◦ above the horizontal a) What is the x component of this force? Answer in units of N. 006 (part 2 of 2) 1.0 points b) What is the y component of this force? Answer in units of N.

Answer 1

a) 6.1 N

Given a force of magnitude F, the horizontal (x) component of the force can be found using the equation:

`F_x = F cos \theta`

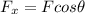
where

F is the magnitude of the force

`\theta` is the angle between the direction of the force and the horizontal

In this problem, we have

F = 6.6 N

`\theta=21.6^(\circ)`

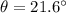
Therefore, the horizontal component is

`F_x = (6.6)(cos 21.6^(\circ))=6.1 N`

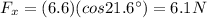
b) 2.4 N

The vertical (y) component of the force can be found using the equation:

`F_y = F sin \theta`

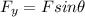
where

F is the magnitude of the force

`\theta` is the angle between the direction of the force and the horizontal

Here we have

F = 6.6 N

`\theta=21.6^(\circ)`

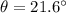
So, the vertical component is

`F_y = (6.6)(sin 21.6^(\circ))=2.4 N`