Question

A company interested in lumbering rights for a certain tract of slash pine trees is told that the mean diameter of these trees is 19 inches with a standard deviation of 2.3 inches. Assume the distribution of diameters is roughly mound-shaped. (a) What fraction of the trees will have diameters between 14.4 and 25.9 inches? 0.75 Incorrect: Your answer is incorrect. (b) What fraction of the trees will have diameters greater than 21.3 inches?

Answer 1

97.5 %

15.7 %

Explanation:

`\mu` = Mean = 19

`\sigma` = Standard deviation = 2.3

a)

`\mu+x\sigma=25.9\\\Rightarrow 19+x* 2.3=25.9\\\Rightarrow x=(25.9-19)/(2.3)\\\Rightarrow x=3`

`\mu-x\sigma=14.4\\\Rightarrow 19-x* 2.3=14.4\\\Rightarrow x=(19-14.4)/(-2.3)\\\Rightarrow x=2`

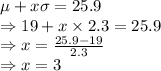
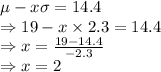
From the empirical rule we get that the percentage of trees between 14.4 and 25.9 inches is 13.6+34.1+34.1+13.6+2.1 = 97.5 %

b)

`\mu+x\sigma=21.3\\\Rightarrow 19+x* 2.3=21.3\\\Rightarrow x=(21.3-19)/(2.3)\\\Rightarrow x=1`

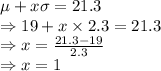
The fraction of tree under 21.3 inches is 34.1.

Hence the fraction of trees above the diameter of 21.3 inches is 13.6+2.1 = 15.7 %