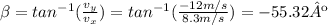Answer:
a)
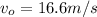
b)

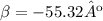
Step-by-step explanation:
From the exercise we know that the ball is thrown at an given angle, strikes the building 18.0 m away, that will be our horizontal displacement. Also, we know whats the final height of the ball which is 8.0 m
a) Given the information that we have we can calculate the initial velocity by solving the following formula

Since we don't know how much time does the ball take to strike the building we need to calculate that first
 (1)
(1)
If we analyze the vertical displacement
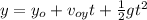

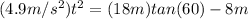
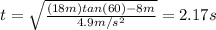
Knowing that time we can calculate the ball's initial velocity from (1)
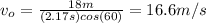
b) To calculate the magnitude and direction of the ball's velocity we need to find the x and y components of velocity

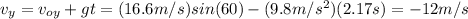
The magnitude of velocity is:
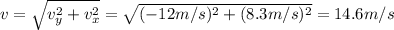
The direction of the ball's velocity is: