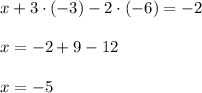Answer:
x = -5, y = -6, z = -3
Explanation:
Given the system of three equations:
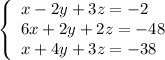
Write the augmented matrix for the system of equations
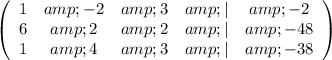
Find the reduced row-echelon form of the augmented matrix for the system of equations:
![\left(\begin{array}{ccccc}1&-2&3&|&-2\\6&2&2&|&-48\\1&4&3&|&-38\end{array}\right)\sim \left(\begin{array}{ccccc}1&-2&3&|&-2\\0&-14&16&|&36\\0&-6&0&|&36\end{array}\right)\sim \left(\begin{array}{ccccc}1&3&-2&|&-2\\0&16&-14&|&36\\0&0&-6&|&36\end{array}\right)]()
Thus, the system of three equations is

From the last equation:
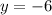
Substitute it into the second equation:
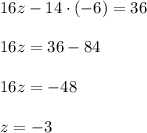
Substitute y = -6 and z = -3 into the first equation: