Question

Height, in meters, is measured for each person in a sample. After the data are collected, all the height measurements

are converted from meters to centimeters by multiplying each measurement by 100. Which of the following statistics
will remain the same for both units of measure?
(A) The mean of the height measurements
(B) The median of the height measurements
(C) The standard deviation of the height measurements
(D) The maximum of the height measurements
(E) The z-scores of the height measurements

Answer 1

(E) The z-scores of the height measurements

Explanation:

Mean is given by

`\bar {x}=(1)/(n)\left(\sum _(i=1)^(n){x_(i)}\right)=(x_(1)+x_(2)+\cdots +x_(n))/(n)`

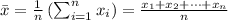
Where,

n = Number of people

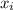`x_(i)` = The heights of people

When converting m to cm the mean would be

`\bar {x}=(1)/(n)\left(\sum _(i=1)^(n){x_(i)}\right)* 100`

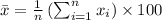
So, the mean would change

The median gives us the middle data value when the data values are in ascending order.

So, the median would change

Standard deviation

`s=\sqrt{(1)/(N-1)\sum_(i=1)^(N)(x_i-\bar{x})^2}`

When converting to centimeters

`s=\sqrt{(1)/(N-1)\sum_(i=1)^(N)\left((x_i-\bar{x})* 100\right)^2`

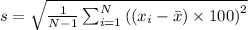
Hence, the standard deviation would change

When converting to centimeters the maximum height in meters would be the maximum height in centimeters also.

The z score is given by

`z=(x-\mu)/(\sigma)`

where,

x = Data point

`\mu` = Mean

`\sigma` = Standard deviation

When converting to centimeters

`z=((x-\mu)* 100)/(\sigma* 100)\\\Rightarrow z=(x-\mu)/(\sigma)`

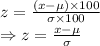
Hence, the z score would remain the same