Answer: a) 0.0000002, b) 15, c) 0.99996.
Explanation:
Since we have given that
n = 500
p = 3% = 0.03
q = 1-0.03 = 0.97
So, we will use "Binomial distribution".
(a) What is the probability that none fail during the warranty period?
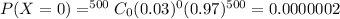
(b) What is the expected number of failures during the warranty period?
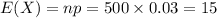
(c) What is the probability that more than 2 units fail during the warranty period?
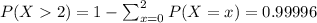
Hence, a) 0.0000002, b) 15, c) 0.99996.