Question

Six less than the quotient of a number and two, increased by ten" when n = 8?

Answer 1

The expression is:
`(n)/(2) + 4`

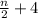
The value at n = 8 is 8

Step-by-step explanation:

1- Getting the expression:

Assume that the variable in the expression is n

Now, we check the givens:

The quotient of n and 2 is translated as
`(n)/(2)`

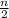
6 less than the quotient means that we will subtract from the quotient

Based on the above, the expression becomes:

`(n)/(2) - 6`

Now, the final given states that the expression obtained from above is increased by 10

This means that we will add 10 to the obtained expression

Based on that, the expression we are looking for is:

`(n)/(2) - 6 + 10 = (n)/(2) + 4`

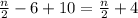
2- Getting the value at n = 8:

To get the value of the expression at n = 8, we will simply substitute in the expression we obtained from part 1

This is done as follows:

`(n)/(2) + 4`

`(8)/(2) + 4 = 4+4 = 8`

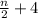
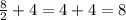
Hope this helps :)