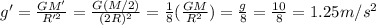Question

Suppose mass and radius of the planet are half and twice that of earth respectively. If acceleration due to gravity of the earth is 10m/s2. Find acceleration due to gravity of that planet?

Answer 1

`1.25 m/s^2`

Step-by-step explanation:

The acceleration of gravity at the surface of a planet planet is given by:

`g=(GM)/(R^2)`

where

G is the gravitational constant

M is the mass of the planet

R is the radius of the planet

Calling M the Earth's mass and R the Earth's radius, the equation above represents the acceleration due to gravity at the Earth's surface, and so

`g=10 m/s^2`

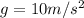
Here we have a planet with:

M' = M/2 (mass is half that of Earth)

R' = 2R (radius is twice that of Earth)

So the acceleration due to gravity of this planet is:

`g'=(GM')/(R'^2)=(G(M/2))/((2R)^2)=(1)/(8)((GM)/(R^2))=(g)/(8)=(10)/(8)=1.25 m/s^2`