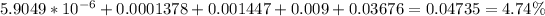Question

trevor is interested in in purchasing the local hardware/sporting goods store in the small town of Dove Creek, Montana. after examining accounting records for the past several years , he found the store has been grossing over $850 per day about 70% of the business day it is open. estimate the probability that the store will gross over $850a) at least 3 out of 5 business daysb) at least 6 out of 10 business daysc) fewer than 5 out of 10 business days

Answer 1

a) 83.69%

b) 84.97%

c) 4.74%

Explanation:

This situation can be modeled with the Binomial Distribution which figures out the likelihood of an event that occurs exactly k times out of n, and is given by

`\large P(k;n)=\binom{n}{k}p^kq^(n-k)`

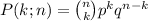
where

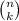`\large \binom{n}{k}`= combination of n elements taken k at a time.

p = probability that the event (“success”) occurs once

q = 1-p

In this case, the event “success” is grossing over $850 one day with a probability of 70% = 0.7

a)

“Estimate the probability that the store will gross over $850 at least 3 out of 5 business days”

Here we want to find

P(3;5)+P(4;5)+P(5;5), that is to say,

`\large \binom{5}{3}0.7^30.3^2+\binom{5}{4}0.7^40.3+\binom{5}{5}0.7^50.3^0=0.3087+0.36015+0.16807 =0.83692 =83.69\%`

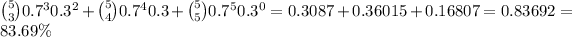
b)

“At least 6 out of 10 business days”

Now we are looking for

P(6;10)+P(7;10)+P(8;10)+P(9;10)+P(10;10)

Applying the same formula with n=10, we get

=0.20012 + 0.26683+0.23347+0.12106+0.82825=0.84973 = 84.97%

c)

“Fewer than 5 out of 10 business days”

P(0;10)+P(1;10)+P(2;10)+P(3;10)+P(4;10) =

`\large 5.9049*10^(-6)+0.0001378+0.001447+0.009+0.03676 = 0.04735 = 4.74\%`