Using the unit circle, you can visualise the secant as follows:
- Draw the vertical line passing trough (1,0)
- Extend the radius until it meets this line at point P
- The length of OP is the secant of your angle.
Since -90 means that the radius points downwards, it means that the radius is vertical as well, and thus it never meets the vertical line through (1,0).
Thus, the secant is not defined at -90.
In fact, if we switch back to the function notation, we can confirm this claim, since we have
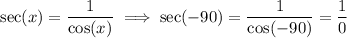
which is undefined.