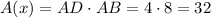Question

Please help me with this question, it's really frustrating me.​

Answer 1

Consider the attached figure. The coordinates of the points are

`A=(-x,0),\quad B=(-x,f(-x)),\quad C=(x,f(x)),\quad D=(x,0)`

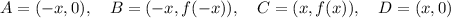
Since f(x) is even, we have

`f(x)=f(-x)=12-x^2`

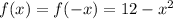
So, the updated coordinates are

`A=(-x,0),\quad B=(-x,12-x^2)),\quad C=(x,12-x^2),\quad D=(x,0)`

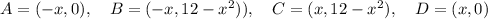
This implies that the rectangle has area

`A(x)=AD\cdot AB = 2x(12-x^2) = -2x^3+24x`

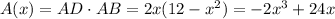
And we want to maximize this function. To so do, let's compute its derivative:

`A'(x)=-6x^2+24=-6(x^2-4)`

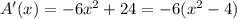
This equals 0 if

`-6(x^2-4)=0 \iff x^2-4=0 \iff x=\pm 2`

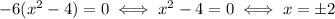
Given the behaviour of the area function (cubic polynomial with negative leading coefficient), the first point is a minimum, and the second point is a maximum. So, for x=2, we have

`A=(-2,0),\quad B=(-2,8)),\quad C=(2,8),\quad D=(2,0)`

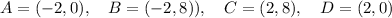
Which yields an area of

`A(x)=AD\cdot AB = 4\cdot 8=32`