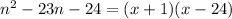Question

Find the factors of nsquare - 23n -24=0

Answer 1

Given a polynomial with degree 2

`ax^2+bx+c`

we can factor it as long as it has solutions. If we have

`ax^2+bx+c=0 \iff x=x_1 \lor x=x_2`

then we have

`ax^2+bx+c=a(x-x_1)(x-x_2)`

In this case, the solutions are given by two numbers that give -24 when multiplied, and 23 when summed. These numbers are clearly 24 and -1.

So, given the roots
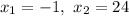`x_1=-1,\ x_2=24`, the factorization would be

`n^2-23n-24=(x+1)(x-24)`

Answer 2

see explanation

Explanation:

Given

n² - 23n - 24 = 0

To factor the quadratic

Consider the factors of the constant term (- 24) which sum to give the coefficient of the n- term (- 23)

The factors are - 24 and + 1, since

- 24 × 1 = - 24 and - 24 + 1 = - 23, thus

(n - 24)(n + 1) = 0 ← in factored form