The required answer is StartFraction negative b plus or minus StartRoot b squared minus 4 a c EndRoot Over 2 a EndFraction, which is
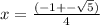
The quadratic equation's general structure is ax² + bx + c = 0 Here the given equation is 4x² + 2x - 1 = 0
These equations can be compared to see that a = 4, b = 2, c = -1
Typically, one uses the following equations to get the roots of a quadratic equation:

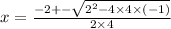
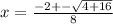



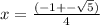
Question:
Which shows the correct substitution of the values a, b, and c from the equation 0 = 4x^(2) + 2x - 1 into the quadratic formula?