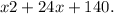Question

Given that f(x) = x2 + 10x + 21 and g(x) = x + 7, find (f•g)(x) and express

the result in standard form.

Answer 1

To find the composition of the functions (f•g)(x) with f(x) =
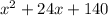`x^2 + 24x + 140`, substitute g(x) into f(x), expand and combine like terms to get (f•g)(x) =
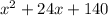`x^2 + 24x + 140`rm.

Step-by-step explanation:

The student is asked to find (f•g)(x), which means we need to compose the functions f(x) and g(x). The function f(x) is given by f(x) =
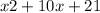`x2 + 10x + 21`tion g(x) is g(x) = x + 7. To find the composition (f•g)(x), we will substitute g(x) into f(x).

Let's calculate (f•g)(x):

1. First, substitute g(x) = x + 7 into f(x): f(g(x)) =
   `(x + 7)2 + 10(x + 7) + 21.`
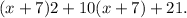
2. Expand the square: f(g(x)) =
   `x2 + 14x + 49 + 10x + 70 + 21.`
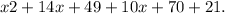
3. Combine like terms: f(g(x)) =
   `x2 + 24x + 140.`

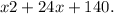
Therefore, the composition of the functions in standard form is (f•g)(x) =
`x2 + 24x + 140.`

Answer 2

`(f.g)x = {x}^(2) + 24x + 140`

Step-by-step explanation:

`given \\ f(x) = x ^(2) + 10x + 21 \: and \: g(x) = x + 7`

`as \: we \: know \: (f.g)x \: is \: same \: as`

`f(g(x))`

`so \:`

`f(x + 7) = ( x + 7) ^(2) + 10(x + 7) + 21`

`f(x + 7) = {x}^(2) + 14x + 49 + 10x + 70 + 21`

`f(x + 7) = x^(2) + 24x + 140`

`therefore`

`(f.g)x = {x}^(2) + 24x + 140`