Question

What is the solution to
∣2⁢x−8∣≤6
?

Answer 1

1 ≤ x ≤ 7

Explanation:

You want to know the solution to |2x-8| ≤ 6.

Setup

This inequality resolves to the compound inequality ...

-6 ≤ 2x -8 ≤ 6

Solution

We note that all of the numbers have 2 as a factor, so we can divide by 2:

-3 ≤ x -4 ≤ 3

Adding 4 gives us the solution.

1 ≤ x ≤ 7

__

Additional comment

Inequalities of the form |a| ≤ b are fully equivalent to the compound inequality -b ≤ a ≤ b, where 'a' represents any expression, and 'b' must be non-negative. The solution set is always the AND of the solutions to the individual inequalities.

If the comparison symbol is reversed, the inequality has a different resolution.

|a| ≥ b ⇒ -b ≥ a OR a ≥ b

These are "shortcut" observations that rely on the fact that |a| is actually a piecewise-defined function:

`|a|=\begin{cases}a&\text{for }a\ge0\\-a&\text{for }a < 0\end{cases}`

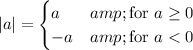
Sometimes, one must be careful of the applicable domain. This is especially true if both 'a' and 'b' contain variable expressions (not just constants).